Fourier transform (FT) is a linear transform which converts a signal from spatial domain into frequency domain. In image processing, FT is mainly used in decomposition of an image into its sine and cosine components. Thus each point in the resulting Fourier image represents a particular frequency contained in the spatial domain. Such is the usefulness of FT that it can determine the relative strength of any periodic data and show periodicity in any input data [1]. The FT of a 2D-image f(x,y) is given by [2]:
One constraint of applying applying FT, however, is computation time, in that at large data input's will take a considerable time to compute [3]. Which is why in 1965, Colley and Tukey developed an algorithm, termed the Fast Fourier Transform (FFT), as a fast and efficient implementation of FT [2]. In the software in which this activity was performed, Scilab 5.4.1, the FFT functions are fft() for 1D signals and fft2() for 2D signals, which is where grayscale images fall under.
In order to test the performance of fft2(), an 128x128 image of a white circle with a black background was synthesized. If we consider an image array to be sectioned in four quadrants, then applying fft2() will interchange the results along the diagonals. The orientation of the original quadrants can be recovered by applying fftshift(), as shown in Figure 1.
Figure 1. (Top Row) Input Image. (Middle Row) Output image after applying FFT2 and (Bottom Row) after applying fftshift. From left to right column; radius (r) = 5, 7, 10, 15 and 20 pixels.
From Figure 1, circles of varying radii were synthesize, ranging from 5 to 20 pixels. The images were converted to double before applying fft2(). fftshift() was them applied to the output to return the quadrants to their original orientation. Based from the results, it can be observed that as the radius of the synthesized aperture increases, the radius of the resulting ring formations in Fourier space decreases. Yet as this occurs, the ring formations steadily become less broken. The broken feature of the ring formations can be attributed to the rasterization of the circle as discussed in Activity 5. As the circle is represented digitally, the smaller the image and the smaller the circle, the more is the circle approximated, resulting in an imperfect circle [4]. In essence, the output is actually a sombrero function [4]. The sombrero function (jinc(t)) can be represented as a Bessel function of the first kind. As Bessel function are analogous to sines, it thus follows that the sombrero function is analogous to the sinc function [5].
where J1 is the Bessel function of the first kind. The distance of the first dark ring from the middle is given by [4]:
where N is the pixel length of the image, N = 128, and r is the radius of the circle. Thus for the 20 pixel radius circle, the distance of the first dark ring to the center pixel is given by x1 = 0.66*128/20 = 4 pixels.
Next an binary image of the letter A was created using paint, to observe the quadrant interchange discussed earlier. This was not shown through the binary image of the circle since the inversion of a circle will still result in a circle.
Figure 2. (a) Input Image, Leftmost. (b) Fourier of (a), Inner Left. (c) After applying fftshift() to (b), Middle.
(d) After applying fft2() to (c). (e) Double application of fft2() to (a)
As can be seen in Figure 2, applying fft2() to the image, interchanges the quadrants or inverts the image, but if fftshift() is applied, the quadrants is reverted back to their original position.
In utilizing FFT for image processing, there are three concepts which will be tackled in this activity; convolution, correlation, and edge detection. Convolution is a linear operation which follows the convolution theorem:
where H, F and G are the transforms of h, f and g, respectively. Convolution can be defined as the imprinting one function unto the other such that the output resembles both functions though not completely. In 2D, the equation for convolution is given as [2]:
Figure 3. Text image
fft2() was then applied to the image. The image was then convolved with the circular apertures shown in Figure 1. Recall that the FT merely translates the signal into frequency space, thus if the quadrants are in there natural orientation, then the fft2() represents the signal in 2D Cartesian coordinates.Thus center values along the image are low frequency, while those nearer the edge are high frequency data. By applying convolution via element-per-element multiplication with a binary circular aperture, we are applying a low-pass filter through the Fourier space, or we are applying a mask. Which is why it can be seen in Figure 4, that as the radius of the aperture increases, the more clearer is the text since more feature data is left unfiltered.
Figure 4. (Top Row) Mask applied. (Bottom Row) Resulting image after convolution.
Image is inverted due to application of fft2() twice and fftshift() once.
Correlation is given by the equation [2] in 2D space:
where p denotes the correlation of the two functions f and g, which denotes the degree of similarity between the two. Thus correlation is mostly used in template matching and pattern recognition. In Scilab, this was implemented by applying fft2() to the text image shown in Figure 5 and the letter texts shown in Figure 6. Element-per-element multiplication between the transform of the letter text and the conjugate transform of the sentence text was performed. The transform of the product was then taken. As shown in Figure 6, results show high correlation between the two images, although clarity varies. It can be observed that the output image is sharper as the font size difference between the two lessens, thus the image is heavily blurred when correlation is taken from the large font text.
Figure 4. Text image
Figure 5. Letter text of varying font size (Top row). Resulting correlation (Bottom Row)
Due to the mechanics behind edge
detection, we can assume that it is a template matching technique. As such, this
can be done by convolution of a 3x3 pattern to the image of interest. Shown in
Figure 7 are the different patterns used in the experiment, but, as can be seen, the dot patter exhibited the best result. This is because the dot pattern showed is independent of direction, as we can see in the horizontal and vertical pattern. To discuss further, if the pattern is centered inside the text or outside, will incur a value of zero due to the summation of the values. If the pattern is centered along the edge of the text, then it will incur a positive value an automatic white. For the other patterns however, like the horizontal patter, if it was centered along the vertical edge, it will result in a value of zero, due the distribution of the values.
Figure 6. (Top Row) Patters, from left to right, horizontal, vertical, diagonal, dot. (Bottom Row) Result after convolving pattern with image in Figure 3 in Fourier space, with the images flipped for comparison.
In this activity I give myself a grade of 10, because I have performed all tasks completely with an understanding and explanation of what was done.









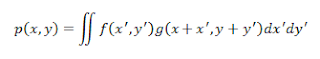



No comments:
Post a Comment