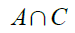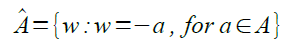Utilizing all the skills acquired in the previous 11 activities, for this activity we were analyze a digital copy of a music sheet and play the notes accordingly using Scilab. For this activity I chose the musical sheet of Frere Jacques:
As one can see, it is a simple music sheet composed of six notes, incorporating Do to La, separated into three different durations (half, quarter, and half-quarter). The first step would be apply a threshold unto the image.
From here I have to determine the location of the notes and the pixel coordinates denoted by the bar to identify the half-quarter notes, I will refer to the notes by their time duration. I decide to tackle the detection of the notes first. Since the notes are nearly circular, they can be isolated by performing a Open morphological operation with a circle of a radius of 1.
FilterBySize() was then applied to remove the small dots and other unnecessary objects, and since the limit of the ledge lines are known, I can impose a zero value to those above it.
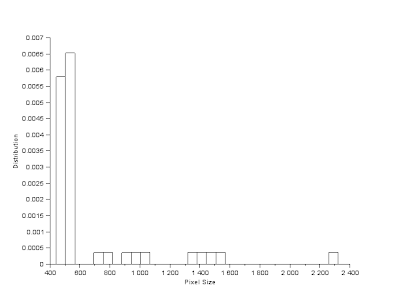
As can be seen the notes has been isolated. I then have to separate the half-note from the others. A key factor in doing this is blob size, as the half notes should have a lesser blob size. Using SearchBlob() as to identify each individual blob and determining their size, I then utilize the histplot() function,
Thus pixel areas less than 100 belong to the half-note, while those above it are to be considered to be of the quarter notes and half-quarter note. Thus by again utilizing the FilterBySize() function, I can separate the two.
For the half note, an Closing morphological operation has to be applied to close the gap between the notes, after doing so the center coordinates for both note categories could be detected by taking the average coordinates of each blob.
With the notes categorized according to height and location, they can now be classified according to their pitch. For this I use the Key of C of the 3rd octave. The only problem now is classifying them according to their duration, with the half notes identified, I now only have to differentiate between the quarter note and half-quarter note. Referring to Figure 1, the half-quarter note is denoted by a bar, thus by determining the column coordinates of the bar and adjusting it accordingly in reference to the last note, notes detected lying along these coordinates are identified as half-quarter notes.
There are two ways in order to do this, one is by applying FilterBySize() once again to isolate the bar,
Or one can apply correlation via Fourier Transform with the bar as the patter,
Thus by reconstructing the notes in audio as sine waves:
note = sine(2*f*t*pi)
I was able to play the music sheet via Scilab. I saved the music file as a video using Windows Live movie Maker following this steps.
I have uploaded the video in youtube.
For this I would like to give myself a grade of 11, for being able to apply the code correspondingly and doing what was required. The additional point was for being able to create a video of the audio file. :)
References:
[1] M. Soriano, 'Activity 12 - Playing notes by Image Processing', Applied Physics 186 manual. UP Diliman, Quezon.
[2]http://www.vaughns-1-pagers.com/music/musical-note-frequencies.htm. Retrieved on August 28, 2013
[3]https://support.google.com/youtube/answer/1696878?topic=2888648&hl=en-GB. Retrieved on August 29, 2013
Figure 1. Image after morphological operation
FilterBySize() was then applied to remove the small dots and other unnecessary objects, and since the limit of the ledge lines are known, I can impose a zero value to those above it.
As can be seen the notes has been isolated. I then have to separate the half-note from the others. A key factor in doing this is blob size, as the half notes should have a lesser blob size. Using SearchBlob() as to identify each individual blob and determining their size, I then utilize the histplot() function,
Figure 2. Pixel area distribution
Thus pixel areas less than 100 belong to the half-note, while those above it are to be considered to be of the quarter notes and half-quarter note. Thus by again utilizing the FilterBySize() function, I can separate the two.
For the half note, an Closing morphological operation has to be applied to close the gap between the notes, after doing so the center coordinates for both note categories could be detected by taking the average coordinates of each blob.
Figure 3. Plot of note coordinates
With the notes categorized according to height and location, they can now be classified according to their pitch. For this I use the Key of C of the 3rd octave. The only problem now is classifying them according to their duration, with the half notes identified, I now only have to differentiate between the quarter note and half-quarter note. Referring to Figure 1, the half-quarter note is denoted by a bar, thus by determining the column coordinates of the bar and adjusting it accordingly in reference to the last note, notes detected lying along these coordinates are identified as half-quarter notes.
There are two ways in order to do this, one is by applying FilterBySize() once again to isolate the bar,
Or one can apply correlation via Fourier Transform with the bar as the patter,
Thus by reconstructing the notes in audio as sine waves:
note = sine(2*f*t*pi)
I was able to play the music sheet via Scilab. I saved the music file as a video using Windows Live movie Maker following this steps.
I have uploaded the video in youtube.
For this I would like to give myself a grade of 11, for being able to apply the code correspondingly and doing what was required. The additional point was for being able to create a video of the audio file. :)
References:
[1] M. Soriano, 'Activity 12 - Playing notes by Image Processing', Applied Physics 186 manual. UP Diliman, Quezon.
[2]http://www.vaughns-1-pagers.com/music/musical-note-frequencies.htm. Retrieved on August 28, 2013
[3]https://support.google.com/youtube/answer/1696878?topic=2888648&hl=en-GB. Retrieved on August 29, 2013