Morphology refers to shape or structure. In image processing, morphological operations are usually performed on binary images, where the data formation of 1's are of interest, so as to improve the image or to extract information, i.e. Isolation and Detection of Spectral line. Thus by this notion, morphological operation affects the shape of the image. In implementing Morphological operations, it is essential to understand set theory.
If assume A to be a set in 2D interger space, and let a be an element of A, then this is represented as,
and if we assume an element b set B which is not found in set A then
If however we want to denote A as a subset of B then
which denotes that all elements of A can be found in B but not otherwise.
Set operations on the other hand include union, which is a set containing all elements contained in the two sets related to the operation, denoted by:
while an intersection denotes a set that contains identical elements between two sets denoted by:
If, however, the two sets are mutually exclusive or that they have no common elements, then the resulting intersection between the two would be result in a null set, shown as:
A complement of A is a set which contains all elements not present in A is denoted as:
the last two set operation are reflection, or flipping the set, and translation, denoted as:
respectively.
In morphological operation, two basic techniques are the dilation and erosion. Dilation is denoted as:
which denotes that the operation is a dilation of A by B. Mathematically, the operation is read such that the structuring element, B, is reflected and will involve all z's such that the intersection of A and the translation of the reflected B does not result in a null set. Thus the effect of Dilation either expands or elongates the image. Erosion on the other hand is denoted by:
which reads as the erosion of A by B. The operation involves all z's such that B translated by z is contained in A or will result such that B will become a subset of A.
Dilation and Erosion can thus be performed manually. In this activity Dilation and Erosion were performed on the following images:
Figure 1. (Leftmost) 5x5 Square (Middle Left) Right Triangle with base = 4 and height = 3 (Middle Right) 10x10 Hollow square with a thickness of 2 pixels and (Rightmost) Plus sign 5 pixels across with 1 pixel thickness
Figure 2. (Leftmost) 2x2 Square (Middle Left) 2x1, (Middle) 1x2 (Middle Right) Plus sign 3 pixels across (Rightmost) 2x2 Diagonal
Implementing each and every Structure element per image, manually through Excel and automatically through Scilab, we compare the results.
Figure 3. Solid Square (Top) Manual Dilation and Erosion. (Bottom) Through Scilab
Figure 4. Triangle (Top) Manual Dilation and Erosion. (Bottom) Through Scilab
Figure 5. Hollow Square (Top) Manual Dilation and Erosion. (Bottom) Through Scilab
Figure 5. Plus (Top) Manual Dilation and Erosion. (Bottom) Through Scilab
As can be seen, the results are exact for the application of Erosion and differ for the Dilation. In my perspective, it seems that the dilation of Scilab did not apply reflection during dilation and as such the difference observed above.
I would like to apologize for the late submission which was caused by faulty internet connection.
Reference:
[1] M. Soriano. "Morphological Operations". Applied Physics 186 2013. University of the Philippines




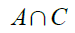


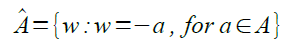












No comments:
Post a Comment